Знаходження площі трапеції за координатами
- Рішення задачі
Знайдіть площу трапеції, вершини якої мають координати (3, 2), (5; 2), (9; 6), (6; 6).

Рішення задачі
В даному уроці представлений приклад рішення задачі В5 на обчислення площі трапеції, яким з успіхом можна скористатися в якості підготовки до ЄДІ з математики.
Для успішного вирішення завдання необхідно знати, що площа трапеції визначається як добуток напівсуми підстав на висоту: 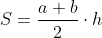 , де
, де  і
і 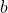 - підстави трапеції, а
- підстави трапеції, а 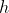 - висота. Згідно з визначенням, трапеція - це чотирикутник, у якого дві сторони паралельні, а дві інші - ні. Паралельні сторони називаються підставами, вони відзначається для наочності червоним кольором. За малюнком визначаються значення підстав заданої трапеції
- висота. Згідно з визначенням, трапеція - це чотирикутник, у якого дві сторони паралельні, а дві інші - ні. Паралельні сторони називаються підставами, вони відзначається для наочності червоним кольором. За малюнком визначаються значення підстав заданої трапеції  і
і 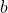 . В ході вирішення також стверджується, що висота трапеції - це відрізок, перпендикулярний її підстав. На малюнку виконується побудова висоти
. В ході вирішення також стверджується, що висота трапеції - це відрізок, перпендикулярний її підстав. На малюнку виконується побудова висоти 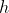 зеленим кольором, а потім обчислюється її довжина як різниця між крайніми зазначеними точками на осі
зеленим кольором, а потім обчислюється її довжина як різниця між крайніми зазначеними точками на осі 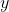 . В результаті, підставивши всі знайдені значення в формулу визначення площі трапеції, визначається шуканий відповідь.
. В результаті, підставивши всі знайдені значення в формулу визначення площі трапеції, визначається шуканий відповідь.

