Пуассі про на распредел е ня, одне з найважливіших розподілів ймовірностей випадкових величин, що приймають цілочисельні значення. Підпорядкована П. р. випадкова величина Х приймає лише невід'ємні значення, причому Х = kc вірогідністю
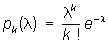, K = 0, 1, 2, ...
(L - позитивний параметр). Свою назву «П. р. »отримало по імені С. Д. Пуассона (1837). Математичне сподівання і дисперсія випадкової величини, що має П. р. з параметром l, рівні l. Якщо незалежні випадкові величини X1 і X2 мають П. р. з параметрами l 1 і l 2, то їх сума X1 + X2 має П. р. з параметрами l 1 + l 2.
У теоретико-імовірнісних моделях П. р. використовується як апроксимує і як точний розподіл. Наприклад, якщо при n незалежних випробуваннях події A 1, ..., An здійснюються з однією і тією ж малою вірогідністю р, то ймовірність одночасного здійснення будь-яких k подій (із загального числа n) приблизно виражається функцією p k (np) ( математичний зміст цього твердження при великих значеннях n и1 / р формулюються Пуассона теоремою ). Зокрема, така модель добре описує процес радіоактивного розпаду і багато ін. Фізичні явища.
Як точне П. р. з'являється в теорії випадкових процесів. Наприклад, при розрахунку навантаження ліній зв'язку зазвичай припускають, що кількості викликів, які надійшли за непересічні інтервали часу, суть незалежні випадкові величини, що підкоряються П. р. з параметрами, значення яких пропорційні довжині відповідних інтервалів часу (див. пуассонівський процес ).
В якості оцінки невідомого параметра l по n наблюденним значенням незалежних випадкових величин X1, ..., X n використовується їх арифметичне середнє X = (X 1 + ... + X n) / n, оскільки ця оцінка позбавлена сістсматіческой помилки і її квадратичне відхилення мінімально (див. Статистичні оцінки ).
Літ .: Гнеденко Б. В., Курс теорії ймовірностей, 5 видавництво., М. - Л., 1969; Феллер Ст, Введення в теорію ймовірностей і її застосування, пер. з англ., 2 вид., т. 1, М., 1967.
Мал. до ст. Пуассона розподіл.
